Expert en Tris
Projet algorithmique
Marc TANGUY Mathieu DECORE
1 Stabilité du tri QuickSort
Pour montrer que QuickSort
n'est pas stable, il nous suffit de le montrer sur un exemple. Soit la liste suivante :
| Albert |
Caroline |
Marc |
Mathieu |
Xavier |
| 14 |
10 |
16 |
10 |
8 |
On cherche à classer cette liste alphabétique d'étudiants par leurs notes. Dès le premier appel de la fonction quicksort, les notes 14 et 10 sont échangées :
| Mathieu |
Caroline |
Marc |
Albert |
Xavier |
| 10 |
10 |
16 |
14 |
8 |
Et le tri se poursuit jusqu'à ce que les notes soient classées :
| Xavier |
Mathieu |
Caroline |
Albert |
Marc |
| 8 |
10 |
10 |
14 |
16 |
On voit clairement sur cet exemple que Mathieu et Caroline ont la même note (10), mais leurs noms ne sont plus classés par ordre alphabétique. On peut donc en conclure que l'algorithme de QuickSort
n'est pas stable.
2 Complexité
On suppose que QuickSort
partitionne le fichier de nombres à trier exactement en deux sous fichiers égaux. Cherchons le nombre de comparaisons effectuées dans ce cas. L'algorithme étant récursif, on choisit de poser une équation de récurrence. Cherchons dans un premier temps la complexité de la fonction partition :
-
Puisque le fichier est partitionné en exactement deux sous fichiers, la boucle
while (T[g] < T[ref]) g++ ; est exécutée n/2 fois (en une ou plusieurs fois). De même, la boucle while (T[d] >= T[ref]) d-- ; est exécutée n/2 fois. Donc il y a n/2 + n/2 = n opérations effectuées par ces deux boucles while, ce qui est le l'ordre de O(n).
- Les échanges effectués et les tests sont en O(1).
La complexité de la fonction partition est donc O(n) + O(1) = O(n) car O(1) << O(n).
Cherchons la complexité de la fonction quicksort. Pour cela, on pose l'équation de récurrence suivante :
Le O(n) est la complexité de la fonction partition. Noter que l'on a négligé le test dans la fonction quicksort, qui est en O(1), donc négligable devant O(n).
On a donc :
T(0) = T(1) = O(1)
T(n) = 2.T(n/2) + n
T(n/2) = 2.T(n/4) + n/2Þ T(n) = 2.(2.T(n/4) + n) = 4.T(n/4 + 2.n)
T(n/4) = 2.T(n/8) + n/4Þ T(n) = 8.T(n/8) + 3.n
:
T(n) = 2i.T(n/2i) + i.n avec 1£ i£ log2 n
Comme on cherche le pire cas, on prend i = log2 n. A la dernière itération, on a :
T(n) = 2m.T(n/2m) + m.n
Or, si n = 2m, alors m = log2 n. Par conséquent :
T(n) = n.T(n/n) + n.log2 n = n.T(1) + n.log2 n
Donc T(n) = n + n.log2 n. On en conclut donc que QuickSort
est en O(n.log2 n).
3 Un quicksort itératif ?
En utilisant une pile, on peut implémenter une version itérative du QuickSort
. En supposant qu'il existent des fonctions permettant d'initialiser une plie (init_pile()), d'empiler (emp()), de dépiler (dep()), et de tester si la pile est vide (pile_vide()), voici l'algorithme itératif de QuickSort
:
emp(g) ;
emp(d) ;
while (!pile_vide())
{
if (d > g)
{
i = partition(a, g, d) ;
emp(g) ;
emp(i - 1) ;
emp(i + 1) ;
emp(d) ;
d = dep() ;
g = dep();
}
else
{
d = dep() ;
g = dep() ;
}
}
4 Partie programmation
On cherche à trouver un nombre d'éléments m tel que QuickSort
soit plus rapide pour un nombre d'éléments à trier supérieur à m qu'un autre tri simple (le tri par insertion par exemple).
4.1 Comparaison du QuickSort
récursif avec le tri par insertion
Après avoir testé différents jeux de données avec les deux algoritmes, il nous est apparu que la rapidité de QuickSort
dépendait de la taille de jeu de données et aussi de l'organisation interne du jeu de donné : trie inverse , randomize etc.
A la vue de cette remarque, nous avons donc choisi de tester à l'aide d'un script shell les différents jeux de données en fonction de la taille et de l'organisation interne du jeu.
4.2 Comparaison avec un jeu de données aléatoires
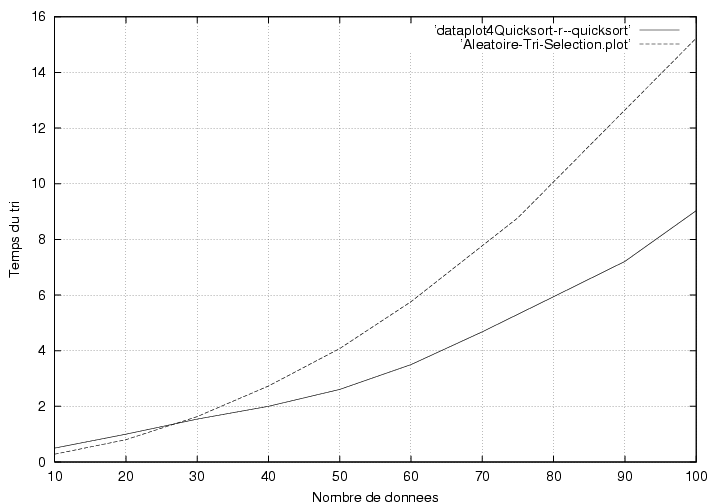
Grâce aux courbes, on distingue le m. Commençons par traiter le cas aléatoire. On trouve m~ 20 :
Figure 1 : Graph de comparaison du tri QuickSort
et tri sélection sur un jeu de données aléatoires.
4.3 Comparaison avec d'autres types de jeux de données
4.3.1 Comparaison avec un jeu de données presque trié
On prend le même script shell en comparant cette fois-ci le QuickSort
itératif
avec le tri sélection, on trouve alors m~ 125 :
Figure 2 : Graph de comparaison du tri QuickSort
et tri sélection sur un jeu de données presque trié.
4.3.2 Comparaison avec un jeu de données trié par ordre décroissant
On trouve avec la même méthode m~ 130 :
Figure 3 : Graph de comparaison du tri QuickSort
et tri sélection sur un jeu de données trié par ordre décroissant.
4.4 Avec le QuickSort
itératif
En utilisant une version itérative du QuickSort
, on obtient les courbes suivantes :
- Pour un jeux de données aléatoires, on trouve m~ 28 :
Figure 4 : Graph de comparaison du tri QuickSort
itératif et tri sélection sur un jeu de données aléatoires.
- Pour un jeu de données presque triées, on trouve m~ 140 :
Figure 5 : Graph de comparaison du tri QuickSort
itératif et tri sélection sur un jeu de données presque triées.
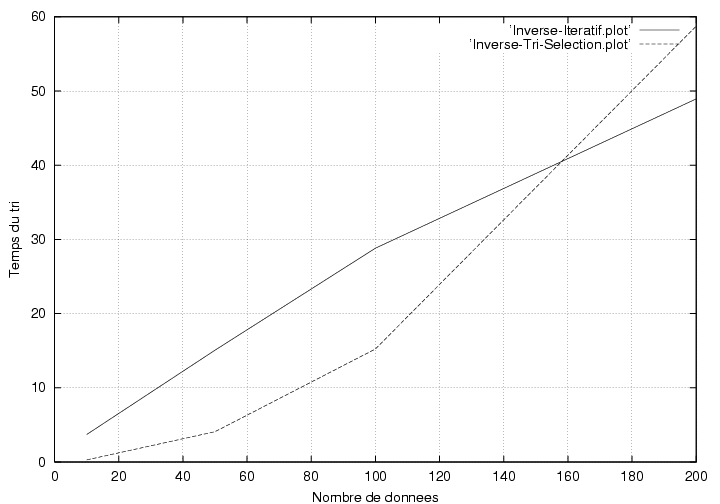
- Pour un jeu de données triées par ordre décroissant, on trouve m~ 155 :
Figure 6 : Graph de comparaison du tri QuickSort
itératif et tri sélection sur un jeu de données trié par ordre décroissant.
On constate que quelque soit le jeu de données utilisé, le QuickSort
itératif est un peu plus lent que le QuickSort
récursif (par rapport à l'algorithme de tri simple choisit). Ceci peut s'expliquer par le fait que pour le QuickSort
itératif, nous implémentons nous même la pile pour empiler les valeurs du sous-fichier à traiter, chose que le programme fait lui même dans la version récursive. Le QuickSort
itératif est donc moins optimisé que le QuickSort
récursif.
4.5 Utilisation d'une file pour implémenter la version itérative de QuickSort
?
L'utilisation d'une file pour la version itérative de QuickSort
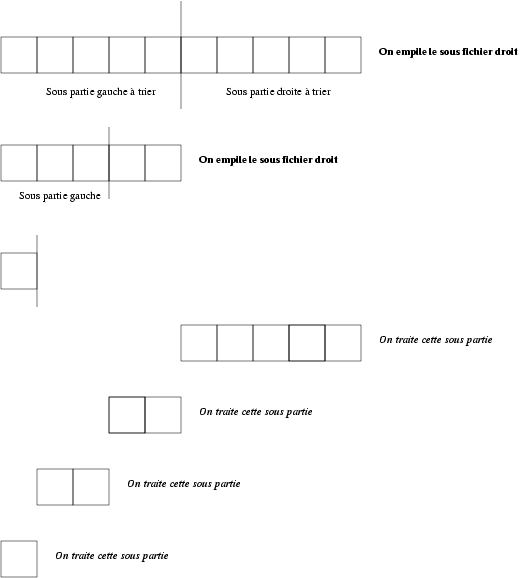
ne changerait pas le problème : en effet, en utilisant une pile, on empile à chaque fois le sous-fichier droit, le sous-fichier gauche, puis on dépile le sous-fichier gauche (le dernier empilé) que l'on traite, avant de traiter le sous-fichier droit. Si on empile à chaque fois, on traite le sous-fichier du sous-fichier gauche, etc. La partie traitée est à chaque fois réduite, mais elle commence toujours à gauche :
Figure 7 : Déroulement de QuickSort
itératif en utilisant une pile.
Lorsqu'on dépile, on a la sous-partie gauche triée, et on n'y revient plus par la suite, puisqu'on traite la sous-partie droite.
En utilisant une file, on traite une sous-partie qui n'est pas contigüe à la précédente, mais comme à chaque fois on ne traite qu'une partie du fichier, cela ne change pas le traitement suivant que l'on utilise une pile ou une file, tout le fichier est traité par petits sous-fichiers :
Figure 8 : Déroulement de QuickSort
itératif en utilisant une file.
Ceci étant dit, une pile est peut-être plus intuitive, plus facile à comprendre.
Ce document a été traduit de LATEX par
HEVEA.
Mathieu DECORE <mdecore@linux-france.org>